Finding Mean, Median, Mode, and Range on the ISEE
All Levels
ISEE Question: The table shows the test scores from ten students in Mr. Smith’s science class.
| 91 | 80 | 77 | 65 | 91 |
| 95 | 100 | 75 | 85 | 92 |
Which of the following statements is true?
A) the range is greater than the mean
B) the mode is greater than the median
C) the median and the mean are equal
D) the median and the mode are equal
Before we can solve this, we need to know how to find mean, median, mode, and range. Memorize these definitions and procedures!
Helpful Tip: Though you should know how to do it, you should NOT always calculate the exact numbers for each statistic. Only do the calculations you need to solve the problem, and avoid long calculations (like finding the mean) whenever possible.
Mean: The average of your set of data. To find it, add together all your numbers and divide by the number of values in your set.
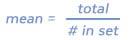
Mean of Mr. Smith’s class = 85.1
65+75+77+80+85+91+91+92+95+100=851
851 ÷ 10 = 85.1
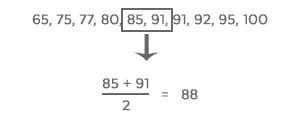
Median: The median is the middle value in your set.
1) Put the values in order from least to greatest
2) Circle the middle number
3) If there are two middle numbers, find the average of those two numbers (the number exactly in between).
median = middle value
Median of Mr. Smith’s class = 88
Mode: The mode is the number that appears the most often. There can be one mode, no mode, or more than one mode.
mode = most common value(s)
Mode of Mr. Smith’s class = 91
Range: The range is the minimum (lowest value) subtracted from the maximum (highest value).
range = maximum – minimum
Range of Mr. Smith’s class = 35
100 – 65 = 35
SOLUTION: Start by finding the mode and median, since those are less time consuming than the mean. We can choose B without having to do any more math!




