Word Problems with Proportional Reasoning on the ISEE
Middle and Upper Level
ISEE Question: If a carpenter decides to cut a 39-inch-long board into two pieces whose lengths have a ratio of 7 to 6, how long should the shorter piece be?
A) 13 in
B) 16 in
C) 18 in
D) 21 in
Helpful Tip: Before you begin solving, don’t forget to estimate the result and have a quick look at the answer choices. The shorter piece is a little less than half of the board, and half of 39 is approximately 20, so D) is too big! On the other hand, A) seems too small. And now, having done almost no math, your chances of getting the right answer between B) and C) are 50%.
Solution:
STEP 1: Ratios are best expressed as fractions: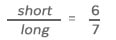
The problem, however, doesn’t give us the length of either piece, but rather of the entire board.
It helps to think about parts. If the long piece is 7 “parts” of the board and the short one is 6 “parts” of the board, then the entire board is 7 + 6 = 13 “parts.”
So a much better ratio to work with would be: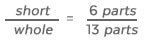
STEP 2: Now let’s express the same ratio in inches: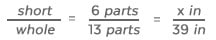
Helpful Tip: Be careful to keep the same “thing” on the top (in this case the short piece) when you express the ratio in different ways!
STEP 3: Let’s cross multiply the two ratios (multiply the numerator of one with the denominator of the other and vice versa and set the two as equal to each other) and solve the resulting equation:
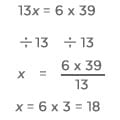
Helpful Tip: Notice that in solving this problem, it’s much faster to simplify the fraction 39/13 than to first multiply 6 * 39 = 234 and then divide 234 by 13 = 18. That trick is a big timesaver in ratio problems.
Before you circle the answer, double-check that you’ve answered what the question was asking! In this case, we solved for the shorter piece, and that is what was needed, but if we had set up the ratio for the longer piece, we would have gotten answer choice D), so be careful!




