Prime Numbers and Prime Factorization on the ISEE
All Levels
ISEE Question: How many distinct prime factors does 150 have?
Solution: Pay attention to the phrasing of the question. The most important words are “distinct” (different from each other) and “prime.”
Prime numbers are those that have exactly two factors (they are divisible by only two numbers): themselves and 1. For example, 7 is a prime number because it is only divisible by 7 and by 1.
NOTE that the number 1 doesn’t fit into the above definition (it has only one factor), and so it is NOT a prime number! That is a very common trap on the ISEE.
So, the list of prime numbers starts with 2 (the only even prime), then 3, 5, 7, 11, 13, 17, 19, 23, and so on …
STEP 1: We’re going to use the line method. Write the number and draw a vertical line next to it.

STEP 2: On the other side of the line, write the smallest prime number that can divide 150. (That is 2.)
STEP 3: Write the quotient below the 150 (it is 75) and next to it, the smallest prime number that divides that.
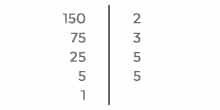
Repeat STEPS 2 and 3 until you reach the number 1 (GAME OVER!).
On the right side of the line you have the prime factorization: 150 = 2 × 3 × 5 × 5
But, of course, we are looking for distinct prime factors, so the answer is “3 distinct prime factors: 2, 3 and 5.”
NOTE that 150 has many other factors that AREN’T prime: 6, 10, 15, 25, 50, 75, and 150. Those can be found by using the factor tree method (see the lesson on “Factoring Numbers on the ISEE”).




