Solving Problems with Exponents on the ISEE
Middle and Upper Level
ISEE Middle-Level Quantitative Comparison:
Column A
-46
Column B
(-4)6
To solve this problem, you must understand exponential notation and exponent negative number rules.
Exponent Basics/ Exponential Notation
An exponent tells you how many times a number (the base) is being multiplied by itself.
46 = 4 × 4 × 4 × 4 × 4 × 4 = 4,096
Do NOT multiply the base by the exponent! 46 ≠ 4 × 6
33 = 3 × 3 × 3 = 27
Helpful Tip: A fraction between 0 and 1 gets smaller as its exponent increases.
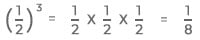
Exponent Negative Number Rules
If you have a negative base and an even exponent, your result will always be positive when you multiply out your exponent, as long as the negative sign and the number are both in parentheses.
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
If you have a negative base in parentheses and an odd exponent, your result will always be negative.
(−4)5 = −1024
If you have a negative number that is not in parentheses, you must calculate the exponent first and then add the negative sign to your product. This is the same as multiplying your product by -1, and exponents come before multiplication in order of operations. The product will be negative with both even and odd exponents.
−44 = −(4 × 4 × 4 × 4) = −256
The solution:
Column A
-4 is not in parentheses, so our product will be negative.
Column B
(-4) is in parentheses and the exponent is even, so our product is positive. B is larger.
Helpful tip: Since you don’t get a calculator, the ISEE rarely asks for time-consuming calculations. Try to answer an exponent question using positive-negative rules or other math reasoning methods before you do any calculations.




