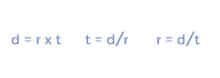Speed and Distance on the ISEE
Middle and Upper Level
ISEE Question: Monica leaves for school at 7:45am and walks the 2-mile distance at a brisk speed of 6 miles per hour. Her father leaves for work at the same time and drives at a speed of 45 miles per hour. They both arrive at their destinations at same time.
Column A
The # of minutes it took Monica to walk to school
Column B
The # of miles her dad drove to work.
Helpful Tip: This is a challenging QUANTATIVE COMPARISON question. It also contains TWO word problems in one, so it requires twice the amount of work and is probably best postponed until you have tried all other problems in this section.
Solution: Begin by underlining the numbers. The time they leave is not relevant but all other numbers are.
STEP 1: Since this is a distance problem, lets breakdown the distance (d), speed/rate (r), and time (t) for both:
MONICA
distance = 2 miles
speed = 6 miles per hour
time = ?
DAD
distance = ?
speed = 45 miles per hour
time = ?
STEP 2: Since we know two of Monica’s numbers and are only missing one, let’s begin with her. We need to apply the distance formula, d = r x t . For Monica, that substitutes to 2 = 6 x t . When we divide by 6 on both sides, we get t = 1/3, but that is in hours! (Helpful Tip: watch out for unit discrepancies as you read the problem and circle the correct units, so you don’t forget to convert.) A third of an hour is 20 minutes.
STEP 3: Now that we know Monica’s time, we also know her dad’s because he arrived at work at the same time. In the distance formula for her dad, though, we’re going to use 1/3 of an hour instead of 20 minutes because his speed is given in miles per hour.
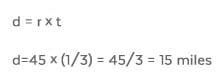
The quantity of Column A is 20, while that of Column B is 15, so the correct answer choice is A).
The distance formula is pretty straightforward, but it appears in three forms based on whether you need to solve for distance, rate or time. Just remember that the “d” is always on top!