Volume of a Three-Dimensional Figure on the ISEE

All Levels

LESSON GOAL: Find the volume of a three-dimensional figure when given its dimensions.

ISEE Lower-Level Volume Question:
The side length of a cube is 4 centimeters. What is its volume?

A) 16 cm3
B) 32 cm3
C) 64 cm3
D) 96 cm3

The solution: V cube = s3

By definition, the length, width, and height of a cube are all equal. The volume of a cube is its side length cubed, or s x s x s. In this case, 4 × 4 × 4 = 64. The volume of the cube is 64 cm3, answer choice C.

ISEE Middle-Level Volume Question:
The dimensions of a rectangular box are 5 in. by 10 in. by 1 foot. What is the volume of the box?

A) 50 in3
B) 300 in3
C) 500 in3
D) 600 in3

The solution: V rectangular prism = l x w x h

Use the formula for volume of a rectangular prism: length X width X height

Step 1: Make sure all your dimensions are in the same unit, converting units as necessary.

1 foot x = 12 in.

Helpful tip: The ISEE will sometimes give you two different units in a problem. Make sure to convert everything to the same unit before you multiply and/or before you choose the correct answer.

Step 2: Multiply length by width by height.

5 × 10 × 12 = 600

The correct answer is D) 600 in3

Helpful tip: To find the volume of any three-dimensional prism or cylinder, use the formula: Volume = (area of the base) x height

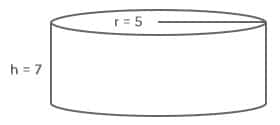
For example, if we know that the radius of a cylinder is 5 and the height is 7, the formula for the volume of the cylinder would be: V cylinder = πr2h = π x 52 x 7 = 175π

View in PDF Format